在一个平面坐标系内,有n个矩形障碍物沿x轴从左向右依次排列(不存在障碍物竖直边重合情况)。某机器人从原点出发,沿障碍物外围向右行进。现根据障碍物的位置信息,寻找机器人的行进路线。
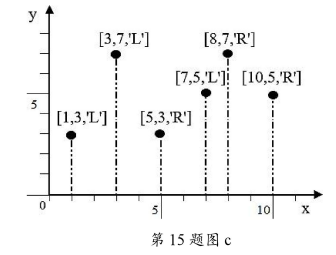
行进路线是由一系列“转折点”组成的序列,每个“转折点”用x、y 坐标值来表示。每个障碍物的位置信息由其左上顶点的坐标及宽度值来表示,如第 15 题图 a 所示,3 个障碍物的位置信息为[[1,3,4],[3,7,5],[7,5,3]],最后得到的行进路线为[[1,3],[3,7],[8,5],[10,0]]。为了简化表示,行进路线中不需要存储连续相同高度的“转折点”,如[1,3],[3,3]两个点只需保留[1,3]。
供参考的做题思路如下:
1. 计算出障碍物左上、右上顶点的坐标,并用“L”和“R”进行标记。根据每个顶点的x坐标值升序排序;
2. 从左往右依次扫描障碍物的顶点。如果遇到左上顶点,将其高度值存储到序列中,若存储高度值的序列最大值发生变化,则产生一个“转折点”;如果遇到右上顶点,从序列中删除其高度值(若有重复值,只删除一次),若删除后存储高度值的序列最大值发生变化,也产生一个“转折点”。
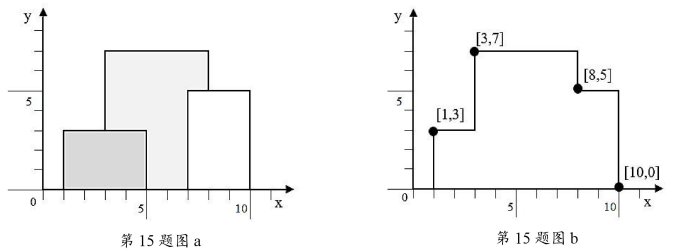
计算障碍物左上、右上顶点的坐标,进行标记;再根据x坐标值升序排序并返回结果,如第 15题图c所示。